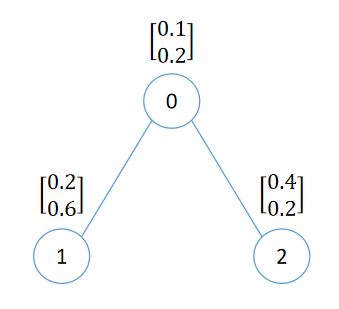
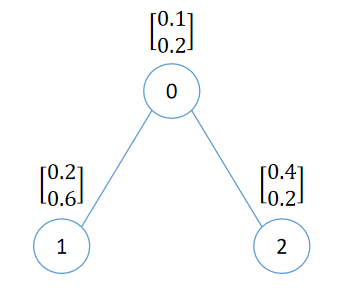
0 前言 今天我们来介绍图论中，我觉得非常简单优雅的算法 PageRank，老样子，我还是会着重使用例子的方式进行介绍，以便大家能够快速清晰地了解这个算法。在这篇文章中，我们用页面来表示点，链接来表示边。 1 简介 PageRank 是由 Google 的创始人拉里·佩奇和谢尔盖·布林在斯坦福大学开发的一种网页排名算法。它的基本思想是通过分析网页之间的链接关系来评估一个页面的重要性。这个算法有两个非常重要的特性： 如果一个页面被很多其他页面链接，则该页面会被认为更重要。 如果一个页面链接到其他页面，则它会将自己的重…
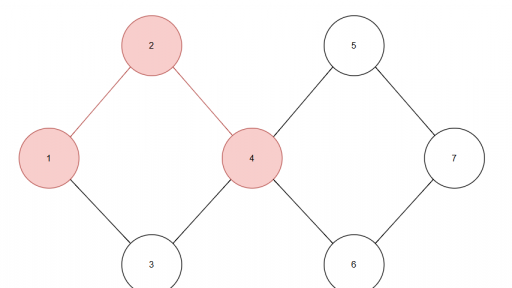
0 前言 我们或多或少都接触过一笔画问题。一笔画问题，即给出一份图，要求使用连续的一笔画过所有的边。换句话说，就是能否通过一笔不间断地画出一个图形，使得每条线段恰好被画过一次。今天我们来看看如何“秒解”这种一笔画问题。 1 欧拉图与欧拉回路 解决一笔画问题的模型是欧拉图与欧拉回路。我们先简单看下定义。 欧拉图：在一个无向图中，如果存在一条回路，这条回路经过图中的每条边恰好一次，并且最终回到起点，那么这条回路被称为欧拉回路，这个图被称为欧拉图。 欧拉回路：如果一个连通的无向图包含至少一条欧拉回路，那么这个图被称为欧拉…
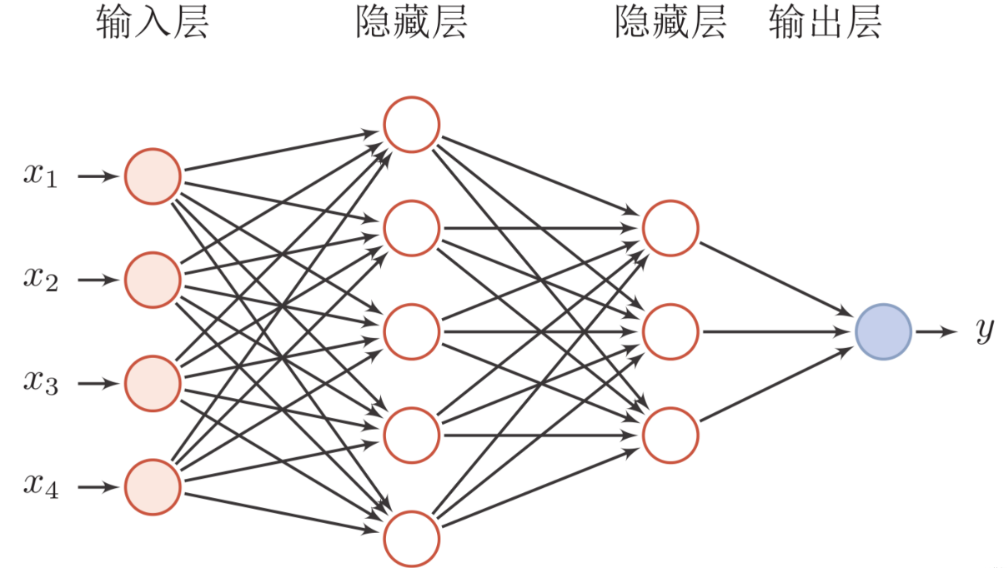
0 前言 我不知道大家有没有和我一样的感受，很多论文里面的神经网络架构往往是通过一系列数学公式来表达，这本身没有问题，但对于初步想要完整了解整个网络架构的人来说，往往就要花比较多的时间去理解公式。 而当我在了解一个神经网络架构的时候，只有完全清楚输入到输出的完整过程，特别是张量维度变化的完整过程，才算认为自己确实了解了这个网络架构。所以我学习的时候往往希望有人能给我个例子，完整展示输入到输出的情况，让我能够更快地去理解论文的架构。我感觉可能也有人和我有同样的需求，所以这篇文章应运而生。这篇文章通过一个的例子，完整地…
0 前言 如果你经常涉及到搜索算法，那么一般对 visited 有一定了解。如果你知道 visited 的作用，却不知道什么时候是正确的进行 visited 标记的时机，这篇文章会给你帮助。 1 visited 概念 在涉及到图或者其他一些结构的搜索时，常常会涉及到节点的重复访问问题，而这个时候，我们常常都会使用 visited 概念来对已经访问过的节点进行标记，从而避免在搜索过程中重复访问同一个节点，避免无限循环或效率降低。 接下来我将从递归和迭代两个场景展示深度优先搜索标记时机的不同（这里以图为例）。 2 递归…
0 前言 我不知道大家有没有和我一样的感受，很多论文里面的神经网络架构往往是通过一系列数学公式来表达，这本身没有问题，但对于初步想要完整了解整个网络架构的人来说，往往就要花比较多的时间去理解公式。 而当我在了解一个神经网络架构的时候，只有完全清楚输入到输出的完整过程，特别是张量维度变化的完整过程，才算认为自己确实了解了这个网络架构。所以我学习的时候往往希望有人能给我个例子，完整展示输入到输出的情况，让我能够更快地去理解论文的架构。我感觉可能也有人和我有同样的需求，所以这篇文章应运而生。这篇文章通过一个的例子，完整地…
0 前言 本文为初步学习神经网络同学而准备，旨在通过最简单直观的方式建立初学者对于神经网络的印象。所以本文的结论和观点主要追求简单直观，而不是严谨。 先举个简单的例子： 假设现在我们有输入 X 与对应输出 Y 的数据一堆 (X, Y) 对如下： { (1, 3), (2, 5), (3, 7), (4, 9), (5, 11), (6, 13), (7, 15), (8, 17), (9, 19), (10, 21) } 现在我们使用架构 f(x) = wx + b 如果我们把 f(x) 当做一个神经网络。那么，神…
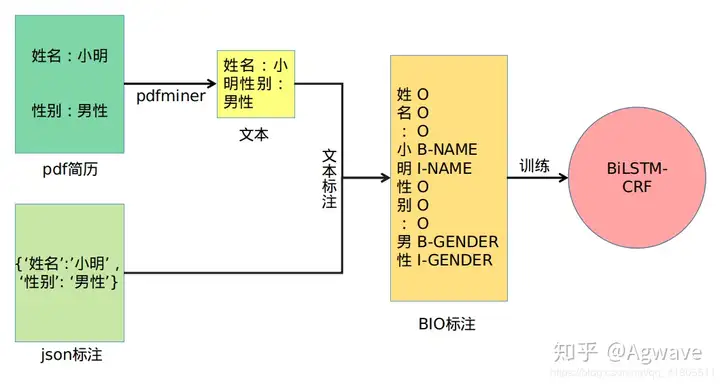
0. 摘要 参加了天池的一个pdf简历信息提取的比赛，这里进行回顾、整理和分享 赛题要求从pdf简历中提取出信息，比如说名字，籍贯等。这里搭建了一个BiLSTM-CRF模型，能够从PDF简历中提取出所需的信息。 模型的线上得分是0.727，排名 21/1200+ 1. 赛题相关 模型目标：pdf简历 --> 类别信息 2. 思路 使用python库pdfminer，将pdf简历中的文本提取出来。利用json标注文件，对提取出来的文本进行匹配和BIO标注，每一个字对应一个标注。最后，将标注后的文本送到BiLSM…
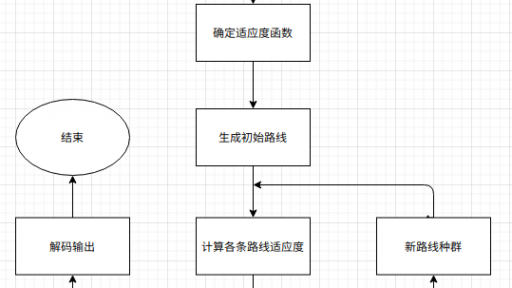
1 问题描述 旅行商问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。 本文章中，城市数据为 127 个城市的 x 和 y 坐标。数据地址见文末。 2 流程图 3 实现细节解释 3.1 路线个体的表示 采用整数编码的方式，将 n 个城市依次编码为 0 到 n-1。对于所给数据而言，将127个城市依次编码为0至126。因此，一条路线可以由一个127维的向量进行表示。 由于路线需要频繁更改，但不会增加或减少城市，这里采用 numpy 作为存储结构。 在实际编码中，为了提高运行效率…
最近评论
njzrqal 发布于 20 小时前（06月16日）
HenryAresy 发布于 2 天前（06月15日）
HenryAresy 发布于 2 天前（06月15日）
MathewCor 发布于 2 天前（06月15日）
MathewCor 发布于 2 天前（06月15日）