0 前言
我们或多或少都接触过一笔画问题。一笔画问题,即给出一份图,要求使用连续的一笔画过所有的边。换句话说,就是能否通过一笔不间断地画出一个图形,使得每条线段恰好被画过一次。今天我们来看看如何“秒解”这种一笔画问题。
1 欧拉图与欧拉回路
解决一笔画问题的模型是欧拉图与欧拉回路。我们先简单看下定义。
欧拉图:在一个无向图中,如果存在一条回路,这条回路经过图中的每条边恰好一次,并且最终回到起点,那么这条回路被称为欧拉回路,这个图被称为欧拉图。
欧拉回路:如果一个连通的无向图包含至少一条欧拉回路,那么这个图被称为欧拉图。
简而言之,从一个点出发,如果可以不重复地走过所有边并回到原点,那么走过的这条路就是欧拉回路。一个图,如果有欧拉回路,那么这个图就是欧拉图。
这里需要留意的点是,一笔画问题有时不要求回到原点,能走完所有边即可。而欧拉回路要求最后是回到原点的。事实上,这种走完所有边但是不走回原点的路径,叫欧拉通路,我们后面会提到。现在我们先专注于欧拉回路问题,后续我们提到的一笔画,都视作要求回到原点的。
2 欧拉定理
2.1 描述
显然,不是对于所有的图,都是可以画出回到原点的一笔画的。既然如此,我们就必须能够判断一个图是否能画出一笔画。现在我就来教教大家如何快速判断。
显然,一个图如果不是连通的,那必然无法一笔画,因此我们的讨论范围是连通图,并且我们把讨论范围定为无向图。
一个连通无向图能不能画出欧拉回路,只有一个很简单的判断条件:所有点的度是偶数。
事实上,一个连通的无向图具有欧拉回路当且仅当图中所有顶点的度数都是偶数,而这,就是图论中著名的欧拉定理。
给我们一个连通无向图,我们判断这个图是否有欧拉回路,只需要判断是不是所有点的度数都是偶数即可。如果所有点的度数都是偶数,那么就存在欧拉回路,这个图是欧拉图。如果并非所有点的度数都是偶数,那么这个图就不是欧拉图。就这么简单。
这时候就有人会问了,为什么是所有点的度数都是偶数,原理是什么?
2.2 证明
必要性:对于一个连通无向图,如果存在欧拉回路,那么所有点的度数都是偶数。
证明过程:对于一个欧拉回路,每当经过一个顶点时(除了起点/终点),都会以一条边进入该顶点,再以另一条边离开该顶点。因此,对于除起点/终点之外的每个顶点,进入的边数等于离开的边数,这些顶点的度数为偶数。由于起点/终点是同一个顶点,它既被进入也被离开,所以它的度数也必须为偶数。
充分性:对于一个连通无向图,如果所有点的度数都是偶数,那么存在欧拉回路。
证明过程:Fleury 算法是一种构造性证明方法,后面讲到 Fleury 算法再具体讲。
3 半欧拉图与欧拉通路
半欧拉图:如果一个无向图中存在一条经过每条边恰好一次的路径,但不一定是闭合的,那么该图称为半欧拉图。
欧拉通路:从一个顶点开始,经过图中的所有边恰好一次到达另一个顶点的路径。
特征:在半欧拉图中,除了起点和终点外,所有其他顶点的度数都是偶数。起点和终点的度数可以是奇数(起点多了一条出的边,终点多了一条入的边)。
4 欧拉通路问题转化为欧拉回路问题
解决欧拉通路问题,我们需要先确定起点和终点,即定位到两个度数为奇数的点,分别作为起点和终点。
之后,为了方便处理欧拉通路问题,我们通常将其转化为欧拉回路问题。方法是添加一条从终点指向起点的边,形成一个欧拉图。这样,原问题就变成了寻找这个新图中的欧拉回路。
总之,求解欧拉通路和欧拉回路最大的不同在于起点和终点的选择,其他的地方都十分相似。
下面我们来看看在欧拉图里找欧拉回路的 Fleury 算法。
5 Fleury 算法
5.1 算法流程
Fleury 算法是一种较为直观的算法,用于判断并找到欧拉通路或回路。该算法的思想是在每一步选择中避免断桥(断桥是指如果删除某条边会导致图分裂成两个或多个不连通部分的边。),即避免在当前阶段移除唯一通往其他未访问顶点的边。具体步骤如下:
- 判断图是否是欧拉图。
- 从任意一个顶点开始。
- 在每一步中,如果当前顶点有多条边可选,选择除了桥以外的任意一条边。桥是指如果移除这条边,图将不再保持连通。
- 删除所选边,并移动到这条边的另一端。
- 重复步骤3和4,直到所有边都被访问过。
5.2 算法例子
看下面这个例子,假设我们从 1 点开始,每次选择非断桥的边走,从 1 走到了 2,从 2 走到了 4,接下来,我们有 3 种走法,走 3 或走 5 或走 6,那么接下来我们应该怎么走呢。
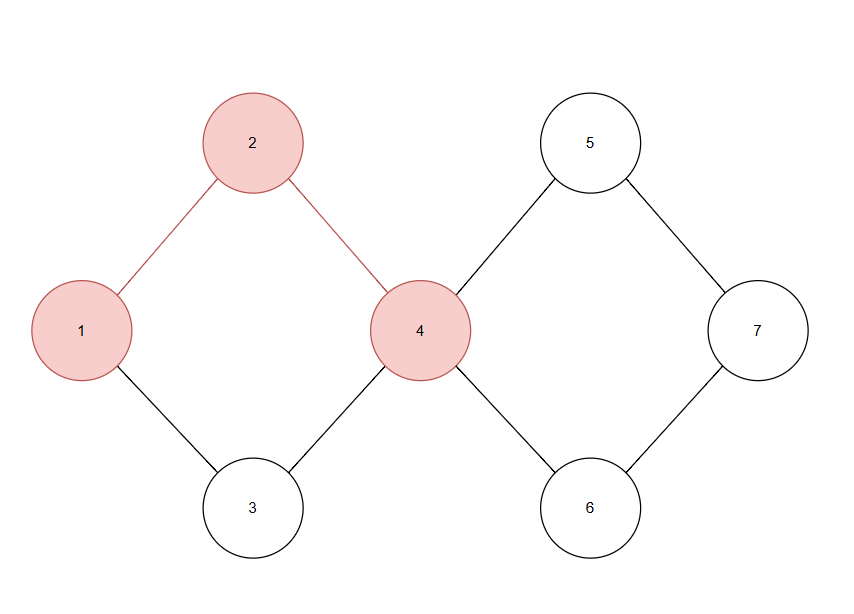
假设我们走了 3,我们会发现,我们接下来只能走到 1,再也无法走到 5、6、7
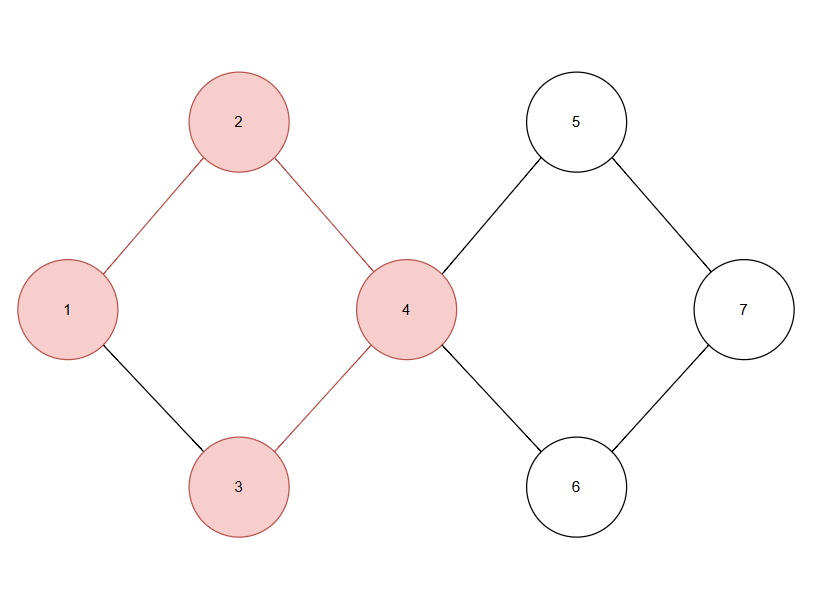
事实上,从 4 到 3 这条边正是断桥,它将未走的边分成了不连通的两部分(1 到 3 这条边与其他未走的边不连通了),导致无法再继续走得到欧拉回路。
但是只要我们选择的是 5 或 6 这两个非断桥边,那么剩下的边仍然是连通的。
希望通过这个例子,你能更了解什么是断桥边,以及在算法过程中避免选择断桥边。
5.3 算法原理
首先我们先证明,如果一个图存在欧拉通路,那么从起点出发,一定有边是非断桥。
反证法:如果从起点出发所有边都是断桥,那么无论走哪一条,都会导致图分裂成多个不连通的图,一定不存在欧拉通路,这与我们的条件(图存在欧拉通路)矛盾。
好了,我们证明了,只要有欧拉通路,从起点出发就一定有非断桥。
接下来我们用归纳法证明算法的可行性。
这个归纳法的核心在于,始终维持了删去边之后图的欧拉性质,并且以当前点为新起点存在欧拉通路回到原起点。
记起点为 \(u\),\(u\) 也是终点。记走过 \(n\) 条边后所处的位置为 \(p_n\),删除走过的 \(n\) 条边后的图为 Gn。
我们来证明:当我们走过 \(n\) 条边时,删除走过的 \(n\) 条边,当前图为 \(G_n\),起点 \(u\) 和当前点 \(p_n\) 度数同时为偶数(当 \(u= p_n\))或同时为奇数(当 \(u \ne p_n\)),非起点和非当前点度数均为偶数,满足半欧拉图性质,必然存在从当前点到起点的欧拉通路,同时对于 \(G_n\) 和当前点(新起点) \(p_n\),一定有非断桥的存在。
- 当我们走过 \(n = 0\) 条边时,删除走过的 \(n = 0\) 条边,当前图为 \(G_0 = G\),起点 \(u\) 和当前点 \(p_0 = u\) 度数同时为偶数(当 \(u= p_0\))或同时为奇数(当 \(u \ne p_0\)),非起点和非当前点度数均为偶数,满足半欧拉图性质,必然存在从当前点到起点的欧拉通路,同时对于 \(G_0\) 和当前点(新起点) \(p_0\),一定有非断桥的边存在。
- 假设走过 \(n = k\) 条边时,删除走过的 \(n = k\) 条边,当前图为 \(G_k\),起点 \(u\) 和当前点 \(p_k\) 度数同时为偶数(当\(u = p_k\))或同时为奇数(当\(u \ne p_k\)),非起点和非当前点度数均为偶数,满足半欧拉图性质,必然存在从点前点到起点的欧拉通路,同时对于 \(G_k\) 和当前点(新起点) \(p_k\),一定有非断桥的便存在。
- 由于对于 \(G_k\) 和当前点 \(p_k\),一定有非断桥的存在,我们选择一条非断桥的边,并删除这条边,得到 \(G_{k+1}\) 和新起点 \(p_{k+1}\)。如果 \(u = p_k\),此时 \(p_k = u\) 度数同时为偶数,那么删除边后,\(u\) 的度由偶数变为奇数,\(p_{k+1}\) 的度由偶数变为奇数。如果 \(u \ne p_k\),此时 \(p_k\),\(u\) 度数同时为奇数,那么删除边后,\(p_k\) 的度由奇数变为偶数,\(p_{k+1}\) 的度由偶数变为奇数。所以,仍然有起点 \(u\) 和当前点 \(p_{k+1}\) 的度数同时为偶数(当 \(u = p_{k+1}\))或同时为奇数(当 \(u \ne p_{k+1}\)),非起点和非当前点度数均为偶数,满足半欧拉图性质,必然存在从当前点到起点的欧拉通路,同时对于 \(G_{k+1}\) 和当前点(新起点) \(p_{k+1}\),一定有非断桥的边存在。
一直这样走,当 n 为所有的边数,便走完了所有的边,即可得到欧拉回路。
为了让大家更简单地理解这个证明过程,可以看下面这种更直观的过程说明。
在最开始,所有点的度数都是偶数,存在欧拉回路。(如果最开始度数不全是偶数,那么欧拉回路便不存在,无需计算)
接下来,选择任意非桥的边走过去并删除这条边,这时,起点和当前所在点的度数变为奇数,其余所有点的度数都是偶数,这时候便满足了半欧拉图的性质,因此必然存在从当前点到原起点的欧拉通路。
我们继续走,选择任意非桥的边走过去并删除这条边,对于除了起点和当前点,我们中间经过的所有点的度数都仍然是偶数,因为经过的点有进就有出,而起点和当前点所在点的度数都为奇数或都为偶数(如果当前点在原起点,则为偶数;如果当前点不在原起点,则为奇数),这时候便满足半欧拉图的性质,必然存在从当前点到原起点的欧拉通路。
一直这样走,直到走完所有的边,便可得到欧拉回路。
这种避免“断桥”的核心在于,始终维持了删去边之后图的欧拉性质,并且以当前点为新起点存在欧拉通路回到原起点。
6 Hierholzer 算法
解决欧拉图的算法还有复杂度更低的 Hierholzer 算法,如果大家感兴趣,请在评论区留言,我再进行补充。

文章评论
Good web site! I truly love how it is easy on my eyes and the data are well written. I am wondering how I could be notified whenever a new post has been made. I have subscribed to your feed which must do the trick! Have a nice day!
I'm curious to find out what blog platform you're working with? I'm experiencing some small security problems with my latest blog and I'd like to find something more risk-free. Do you have any recommendations?
I'm still learning from you, while I'm making my way to the top as well. I certainly liked reading everything that is posted on your blog.Keep the information coming. I enjoyed it!
Today, I went to the beach front with my kids. I found a sea shell and gave it to my 4 year old daughter and said "You can hear the ocean if you put this to your ear." She placed the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear. She never wants to go back! LoL I know this is entirely off topic but I had to tell someone!
What’s Going down i am new to this, I stumbled upon this I have found It absolutely useful and it has helped me out loads. I hope to contribute & assist other customers like its helped me. Good job.
When I initially commented I clicked the "Notify me when new comments are added" checkbox and now each time a comment is added I get four e-mails with the same comment. Is there any way you can remove me from that service? Thanks a lot!
I¦ve been exploring for a little bit for any high-quality articles or weblog posts in this kind of area . Exploring in Yahoo I eventually stumbled upon this web site. Reading this information So i¦m glad to show that I have a very good uncanny feeling I found out just what I needed. I such a lot surely will make certain to don¦t forget this site and give it a glance regularly.
I¦ll right away clutch your rss feed as I can not find your e-mail subscription link or newsletter service. Do you've any? Please let me know so that I may subscribe. Thanks.
You completed several nice points there. I did a search on the topic and found a good number of people will consent with your blog.
This is a very good tips especially to those new to blogosphere, brief and accurate information… Thanks for sharing this one. A must read article.
Hello, i think that i saw you visited my site so i came to “return the favor”.I'm trying to find things to enhance my site!I suppose its ok to use a few of your ideas!!
You really make it seem so easy with your presentation but I find this matter to be really something that I think I would never understand. It seems too complex and extremely broad for me. I am looking forward for your next post, I will try to get the hang of it!
I want reading and I believe this website got some truly useful stuff on it! .
Very interesting information!Perfect just what I was looking for! "All the really good ideas I ever had came to me while I was milking a cow." by Grant Wood.
Hello! I could have sworn I've been to this blog before but after reading through some of the post I realized it's new to me. Anyways, I'm definitely happy I found it and I'll be bookmarking and checking back often!
Your style is so unique compared to many other people. Thank you for publishing when you have the opportunity,Guess I will just make this bookmarked.2
I enjoy the efforts you have put in this, appreciate it for all the great blog posts.
Some truly good articles on this web site, thankyou for contribution.
But a smiling visitor here to share the love (:, btw outstanding style. "Treat the other man's faith gently it is all he has to believe with." by Athenus.
I loved as much as you'll receive carried out right here. The sketch is tasteful, your authored material stylish. nonetheless, you command get bought an impatience over that you wish be delivering the following. unwell unquestionably come more formerly again since exactly the same nearly a lot often inside case you shield this increase.
I carry on listening to the news broadcast speak about receiving free online grant applications so I have been looking around for the most excellent site to get one. Could you tell me please, where could i find some?
Good info. Lucky me I reach on your website by accident, I bookmarked it.
Excellent read, I just passed this onto a colleague who was doing a little research on that. And he just bought me lunch because I found it for him smile So let me rephrase that: Thank you for lunch!
Do you mind if I quote a few of your posts as long as I provide credit and sources back to your website? My blog is in the very same area of interest as yours and my visitors would truly benefit from a lot of the information you present here. Please let me know if this okay with you. Appreciate it!
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post…
I got what you intend,bookmarked, very nice site.
Hello. Great job. I did not expect this. This is a excellent story. Thanks!
I got what you intend,saved to my bookmarks, very decent internet site.
I have been examinating out some of your posts and i must say pretty nice stuff. I will definitely bookmark your blog.
I’ve read several good stuff here. Certainly worth bookmarking for revisiting. I wonder how much effort you put to create such a wonderful informative website.
Hello there! I could have sworn I've been to this site before but after reading through some of the post I realized it's new to me. Anyhow, I'm definitely happy I found it and I'll be bookmarking and checking back often!
I like the efforts you have put in this, thank you for all the great posts.
hello!,I really like your writing so a lot! percentage we keep in touch extra approximately your post on AOL? I require a specialist on this area to solve my problem. Maybe that's you! Taking a look ahead to peer you.
Do you have a spam issue on this blog; I also am a blogger, and I was curious about your situation; many of us have developed some nice methods and we are looking to trade strategies with others, why not shoot me an e-mail if interested.