1 问题描述
旅行商问题:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
本文章中,城市数据为 127 个城市的 x 和 y 坐标。数据地址见文末。
2 流程图
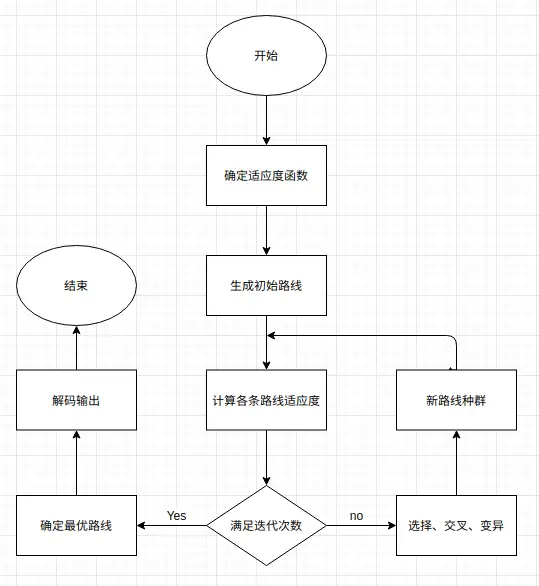
3 实现细节解释
3.1 路线个体的表示
采用整数编码的方式,将 n 个城市依次编码为 0 到 n-1。对于所给数据而言,将127个城市依次编码为0至126。因此,一条路线可以由一个127维的向量进行表示。
由于路线需要频繁更改,但不会增加或减少城市,这里采用 numpy 作为存储结构。
在实际编码中,为了提高运行效率,所有路线被编码成一个2维 numpy 数组,每一行表示一条路线。如,2 条 10 个城市的路线可以表示为:
\(\begin{bmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 & 1
\end{bmatrix}\)
在代码中,我将路线种群的数量设置为 100,而城市个数为 127,故所有路线可以表示为一个 (100, 127) 的 numpy 数组。
3.2 距离与适应度函数
路线距离和适应度是衡量路线优良的指标,必须好好理解。
距离定义比较简单,两个城市m和n之间的距离定义为二维空间欧氏距离:
\(d_{mn}=\sqrt{{(x_m-x_n)}^2 + {(y_m-y_n)}^2}\)
则某一路线的总距离定义为:
\(D=\sum_{j=1}^{n}l_j\)
其中,\(l_j\) 为路线中第 \(j\) 个城市到第 \(j+1\) 个城市的距离( 1 为起始城市),\(l_n\) 为路线中最后一个城市到第一个城市的距离。
例如,对于路线: 1 0 3 2
其路线总距离
\(D=l_1+l_2+l_3+l_4=d_{10}+d_{03} + d_{32} + d_{21}\)
在实际编码中,我们预先计算出了一个城市距离矩阵(对称矩阵),第 i 行 j 列的元素表示城市 i 到城市j之间的距离。
这样预先处理的好处是,避免在后面迭代的过程中进行无意义的重复计算。
例如,4 个城市的城市距离矩阵为:
\(\begin{bmatrix}
d_{00} & d_{01} & d_{02} & d_{03} \\
d_{10} & d_{11} & d_{12} & d_{13} \\
d_{20} & d_{21} & d_{22} & d_{23} \\
d_{30} & d_{31} & d_{32} & d_{33}
\end{bmatrix}\)
适应度函数 f 取距离的倒数:
\(f=\frac{1}{D}\)
3.3 路线初始化
这里初始种群为随机生成的 100 条路线。 使用 np.random.choice 生成 0 至 n-1 的不重复的长度为 n 的 numpy 数组。
3.4 选择
个体路线适应度越高,其被选择的机会就越多。故此处采用与适应度成比例的概率方法进行选择。
具体地说,就是首先计算群体中所有个体适应度的总和,再计算每个个体的适应度所占的比例,并以此作为相应的选择概率。然后采用轮盘赌方法进行 100 次带概率的随机选择。
3.5 交叉
交配操作是遗传算法中最主要的遗传操作。这里可能是相对比较难理解的,我理解的时候也是花了一些时间,我这里会用例子进行详细解释。
这里采用基于部分映射的交配法:
产生一个随机数,确定交叉的起始位置,对起始位置及之后的位置进行交换,并放在首位,然后再从各自的路径中按顺序填充未出现过的数字。
例如,当随机数为 4 时,起始位置取 4,交叉结果如下(以10个城市为例):
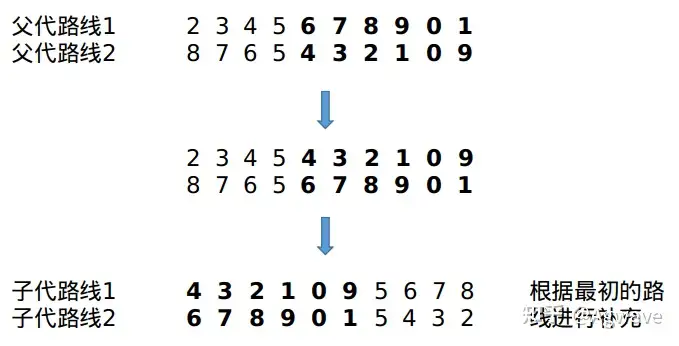
对所有路线两两进行交叉操作。如路线 0 和路线 1,路线 2 和路线 3,以此类推。
3.6 变异
变异操作是按向量维度进行的,即把某一维的内容进行变异。变异操作同样也是随机进行的。一般而言,变异概率都取得较小,这里概率取0.01,采取对于一个路线个体随机选取两个城市进行交换的策略。如下:
父代路径: 0 8 6 5 1 7 2 9 3 4 0
子代路径: 0 8 6 9 1 7 2 5 3 4 0
3.7 最优路线的保存
我设置的最大迭代次数是 100000,每一次迭代之后,都会保存最优的路线。如果连续2000次迭代之后,最优路线都没有改变,就停止迭代。输出最优的路线。
4 运行结果展示
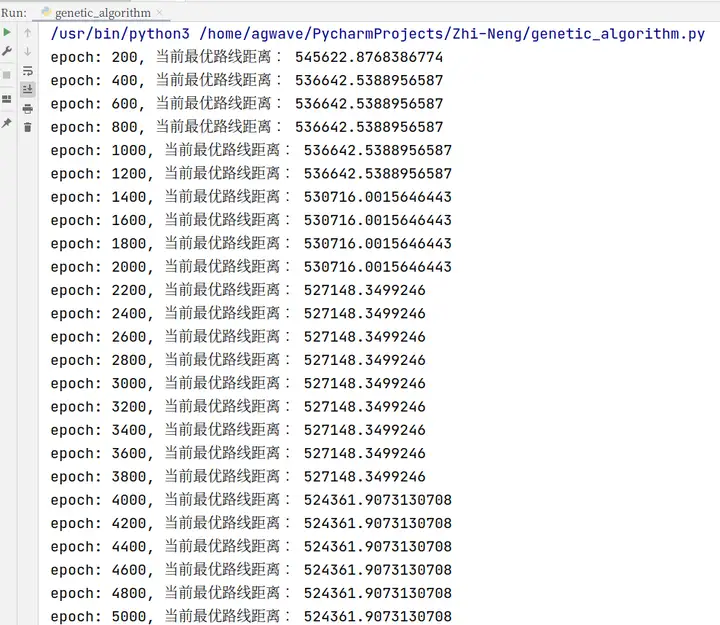
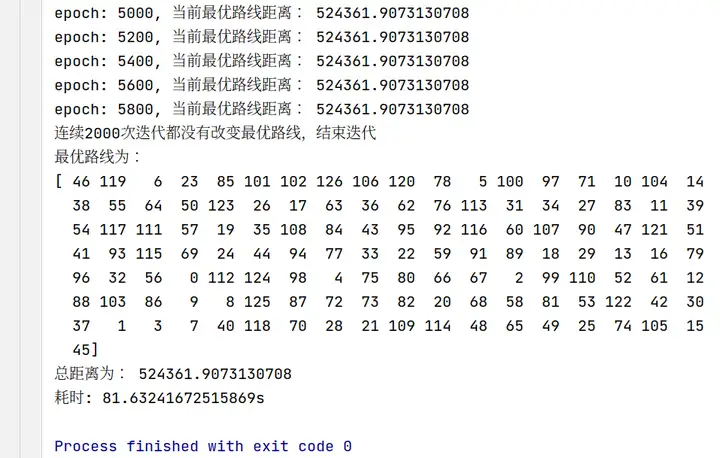
(每个城市编号加一后即为原来数据城市编号)
5 代码与数据
6 代码使用方法
只需修改数据导入方式,将数据导入 cities 变量,即可运行。当然最好也相应修改一下main函数中的参数。

文章评论
Simply wanna say that this is invaluable, Thanks for taking your time to write this.
Lovely just what I was searching for.Thanks to the author for taking his time on this one.
Hi, I think your site might be having browser compatibility issues. When I look at your website in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, fantastic blog!
Great write-up, I'm normal visitor of one's blog, maintain up the excellent operate, and It's going to be a regular visitor for a long time.
The root of your writing while appearing reasonable initially, did not settle well with me after some time. Someplace throughout the paragraphs you were able to make me a believer but just for a short while. I however have a problem with your jumps in assumptions and you might do well to help fill in all those breaks. In the event that you can accomplish that, I could definitely end up being fascinated.
Hey very cool site!! Man .. Excellent .. Wonderful .. I will bookmark your blog and take the feeds alsoKI am satisfied to find numerous useful information right here in the post, we'd like develop extra techniques in this regard, thank you for sharing. . . . . .
I really appreciate this post. I have been looking all over for this! Thank goodness I found it on Bing. You have made my day! Thanks again
Hi! I'm at work surfing around your blog from my new iphone 4! Just wanted to say I love reading your blog and look forward to all your posts! Carry on the great work!
Have you ever considered about adding a little bit more than just your articles? I mean, what you say is important and all. But think of if you added some great images or video clips to give your posts more, "pop"! Your content is excellent but with pics and clips, this blog could definitely be one of the greatest in its field. Terrific blog!
Hello. excellent job. I did not anticipate this. This is a fantastic story. Thanks!
of course like your web site but you need to check the spelling on quite a few of your posts. Many of them are rife with spelling problems and I find it very bothersome to tell the truth nevertheless I’ll surely come back again.
I have read some good stuff here. Definitely worth bookmarking for revisiting. I surprise how much effort you put to create such a fantastic informative website.
Attractive section of content. I just stumbled upon your site and in accession capital to assert that I acquire in fact enjoyed account your blog posts. Anyway I will be subscribing to your feeds and even I achievement you access consistently rapidly.
I admire your work, thankyou for all the interesting blog posts.
It’s actually a cool and helpful piece of information. I am glad that you shared this useful info with us. Please keep us up to date like this. Thanks for sharing.
I like what you guys are up too. Such intelligent work and reporting! Keep up the excellent works guys I have incorporated you guys to my blogroll. I think it will improve the value of my web site :)
Very interesting information!Perfect just what I was looking for! "If you want to test your memory, try to recall what you were worrying about one year ago today." by Rotarian.
Great – I should certainly pronounce, impressed with your website. I had no trouble navigating through all tabs as well as related info ended up being truly easy to do to access. I recently found what I hoped for before you know it in the least. Quite unusual. Is likely to appreciate it for those who add forums or anything, website theme . a tones way for your customer to communicate. Nice task..
Hey very cool site!! Man .. Beautiful .. Amazing .. I will bookmark your web site and take the feeds also…I am happy to find so many useful information here in the post, we need work out more techniques in this regard, thanks for sharing. . . . . .
I savor, result in I found exactly what I was having a look for. You've ended my 4 day long hunt! God Bless you man. Have a great day. Bye
Hi, I think your site might be having browser compatibility issues. When I look at your website in Safari, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, fantastic blog!
hi!,I really like your writing very a lot! proportion we communicate extra about your article on AOL? I require an expert on this area to unravel my problem. Maybe that is you! Looking ahead to see you.
Can I just say what a relief to find someone who actually knows what theyre talking about on the internet. You definitely know how to bring an issue to light and make it important. More people need to read this and understand this side of the story. I cant believe youre not more popular because you definitely have the gift.
Thanks for any other informative blog. Where else may I get that type of info written in such a perfect approach? I have a venture that I'm just now operating on, and I've been at the look out for such info.
I have been absent for a while, but now I remember why I used to love this web site. Thank you, I¦ll try and check back more often. How frequently you update your website?
I gotta favorite this web site it seems very helpful invaluable
Simply a smiling visitant here to share the love (:, btw outstanding style. "He profits most who serves best." by Arthur F. Sheldon.
Im not sure the place you're getting your information, but great topic. I must spend a while finding out much more or figuring out more. Thanks for fantastic info I was on the lookout for this information for my mission.
It's best to take part in a contest for one of the best blogs on the web. I'll suggest this website!
An impressive share, I simply given this onto a colleague who was doing just a little analysis on this. And he the truth is purchased me breakfast because I discovered it for him.. smile. So let me reword that: Thnx for the treat! But yeah Thnkx for spending the time to discuss this, I feel strongly about it and love studying extra on this topic. If possible, as you develop into expertise, would you thoughts updating your weblog with more particulars? It is extremely helpful for me. Massive thumb up for this blog put up!
I've been browsing online more than three hours today, yet I never found any interesting article like yours. It’s pretty worth enough for me. In my view, if all web owners and bloggers made good content as you did, the internet will be a lot more useful than ever before.
You are my inspiration, I possess few blogs and rarely run out from brand :). "'Tis the most tender part of love, each other to forgive." by John Sheffield.
You completed some fine points there. I did a search on the topic and found the majority of folks will consent with your blog.
You are my intake, I have few web logs and sometimes run out from post :). "Follow your inclinations with due regard to the policeman round the corner." by W. Somerset Maugham.