0 前言
我不知道大家有没有和我一样的感受,很多论文里面的神经网络架构往往是通过一系列数学公式来表达,这本身没有问题,但对于初步想要完整了解整个网络架构的人来说,往往就要花比较多的时间去理解公式。
而当我在了解一个神经网络架构的时候,只有完全清楚输入到输出的完整过程,特别是张量维度变化的完整过程,才算认为自己确实了解了这个网络架构。所以我学习的时候往往希望有人能给我个例子,完整展示输入到输出的情况,让我能够更快地去理解论文的架构。我感觉可能也有人和我有同样的需求,所以这篇文章应运而生。这篇文章通过一个的例子,完整地展示 GCN 架构是如何将输入逐步转换为输出的。
如果大家觉得这种通过例子学习方式对自己帮助,请点赞或者评论让我知道,我会继续更新这种类型的文章。
1 GCN 层公式
一个 GCN 架构的是多个 GCN 层的堆叠,输入一层一层传播形成输出,接下来我们先围绕 GCN 层来说。
首先我们需要知道的是 GCN 前向传播的过程,就是在不断地在更新节点特征的过程。GCN 层的传播公式可以表述为:
\(H^{(l+1)} = \sigma (\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)})\)在这个公式中:
- \(H^{(l)}\) 表示第 \(l\) 层的节点特征矩阵,其维度通常是 \(N \times D_l\),其中 \(N\) 是节点的数量,\(D_l\) 是该层的特征维度。
- \(H^{(l+1)}\) 表示 \(l+1\) 层的输出特征矩阵,维度为 \(N \times D_{l+1}\)。
- \(W^{(l)}\) 是第 \(l\) 层的权重矩阵,用于执行线性变换,其维度为 \(D_l \times D_{l+1}\)。
- \(\sigma\) 是一个非线性激活函数,如 ReLU,它被应用于每个节点的特征上。
- \(\widetilde{A}\) 是邻接矩阵 \(A\) 的修正版本,通常会在 \(A\) 中添加自连接(即对角矩阵 \(I\),使得每个节点与其自身相连),表示为 \(\widetilde{A} = A + I\)。
- \(\widetilde{D}\) 是 \(\widetilde{A}\) 的度矩阵,即 \(\widetilde{D}_{ii} = \sum_j \widetilde{A}_{ij}\) , 并且\(\widetilde{D}^{-\frac{1}{2}}\) 是 \(\widetilde{D}\) 的平方根的逆矩阵,用于归一化,确保节点度数的影响在信息传递过程中得以平衡。
这个过程描述了在 GCN 层中,如何通过邻居节点的特征和权重矩阵,以及归一化的邻接关系来更新每个节点的特征表示。每一层的输出成为下一层的输入,从而允许信息在整个图结构中传播。可以直观理解为,更新当前节点的特征,需要同时考虑该节点的邻接关系以及邻居节点的特征。
2 GCN 层例子
假设现在有一份图数据如下
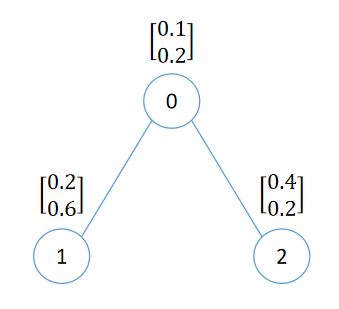
我们来看看对于这个图数据,\(H^{(l+1)} = \sigma (\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} H^{(l)} W)\) 中右边的值都是什么。
从图中可以看到,
节点 0 的特征为 \(X_0 = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix}\)
节点 1 的特征为 \(X_1 = \begin{bmatrix} 0.2 \\ 0.6 \end{bmatrix}\)
节点 2 的特征为 \(X_2 = \begin{bmatrix} 0.4 \\ 0.2 \end{bmatrix}\)
所以特征矩阵 \(X = \begin{bmatrix} 0.1 & 0.2 \\ 0.2 & 0.6 \\ 0.4 & 0.2 \end{bmatrix}\)
由上图的拓扑结构,可知邻接矩阵 A = \(\begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}\)
则 \(\widetilde{A} = A + I = \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} + \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}\)
由 \(\widetilde{D}_{ii} = \sum_j \widetilde{A}_{ij} \),得到 \(\widetilde{D} = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{bmatrix}\),进而 \(\widetilde{D}^{-\frac{1}{2}} = \begin{bmatrix} \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix}\)
由于 \(\widetilde{A}\) 和 \(\widetilde{D}^{-\frac{1}{2}}\) 都是固定的,我们不妨记 \(\widehat{A} = \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}}\),则有 \(H^{(l+1)} = \sigma (\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}) = \sigma (\widehat{A} H^{(l)} W^{(l)})\)。
\(\widehat{A} = \widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} =\begin{bmatrix} \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix}
\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}
\begin{bmatrix} \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & \frac{1}{\sqrt{2}} \end{bmatrix} =
\begin{bmatrix} \frac{1}{3} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} & \frac{1}{2} & 0 \\ \frac{1}{\sqrt{6}} & 0 & \frac{1}{2} \end{bmatrix}\)
假设我们现在 \(l = 0\), 此时那么 \(H^{(l)} = H^{(0)}\),而 \(H^{(0)}\) 即是初始的特征矩阵 X。
初始节点特征维度为 2,所以 \(D_0 = 2\)。假设转换后的隐藏层特征维度 \(D_1 = 3\),那么 \(W^{(0)}\) 权重矩阵的维度为 \((D_0, D_1) = (2, 3)\)。
\(W^{(0)}\) 是随机初始化的参数矩阵,我们就设 \(W^{(0)} = \begin{bmatrix} 0.5 & 0.5 & 0.5 \\ 0.5 & 0.5 & 0.5 \end{bmatrix}\)。
我们现在开始来更新节点的特征。此时 \(H^{(0)} = X = \begin{bmatrix} 0.1 & 0.2 \\ 0.2 & 0.6 \\ 0.4 & 0.2 \end{bmatrix}\)
\(H^{(1)} = \sigma (\widetilde{D}^{-\frac{1}{2}} \widetilde{A} \widetilde{D}^{-\frac{1}{2}} H^{(0)} W^{(0)}) =\sigma (\widehat{A} H^{(0)} W^{(0)}) \\ =
\sigma (\widehat{A} X W^{(0)}) \\ =
\sigma \left (
\begin{bmatrix} \frac{1}{3} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} & \frac{1}{2} & 0 \\ \frac{1}{\sqrt{6}} & 0 & \frac{1}{2} \end{bmatrix}
\begin{bmatrix} 0.1 & 0.2 \\ 0.2 & 0.6 \\ 0.4 & 0.2 \end{bmatrix}
\begin{bmatrix} 0.5 & 0.5 & 0.5 \\ 0.5 & 0.5 & 0.5 \end{bmatrix}
\right )\)
按上述值进行计算即可得到经过一层 GCN 层的输出 \(H^{(1)}\)。
至此,我们已经完全清楚了公式中每个变量的含义、维度、信息等,通过一层 GCN,我们得到了新的隐藏层特征 \(H^{(1)}\)。
3 多层 GCN 层的堆叠
前面我们已经完全清楚了公式中每个变量的含义、维度、信息等,通过一层 GCN,我们得到了新的隐藏层特征 \(H^{(1)}\)。而 GCN 神经网络就是 GCN 层的堆叠,从 \(H^{(0)}\) (即 \(X\)) 计算得到 \(H^{(1)}\),从 \(H^{(1)}\) 计算得到 \(H^{(2)}\),一层一层往下计算。
比如说对于两层 GCN,公式就是 \(H^{(2)} = \sigma (\widehat{A} H^{(1)} W^{(1)}) = \sigma (\widehat{A} (\sigma (\widehat{A} H^{(0)} W^{(0)})) W^{(1)})\)。
好了,这篇文章到这里就要结束了。最后再留一个问题,输出 \(H^{(l+1)}\) 的维度是由哪个变量决定的呢?

文章评论
Really clear site, appreciate it for this post.
certainly like your web-site however you need to check the spelling on quite a few of your posts. Several of them are rife with spelling problems and I to find it very bothersome to tell the reality nevertheless I will definitely come again again.
I get pleasure from, lead to I found just what I was taking a look for. You've ended my four day lengthy hunt! God Bless you man. Have a nice day. Bye
The subsequent time I read a weblog, I hope that it doesnt disappoint me as much as this one. I mean, I know it was my option to learn, but I really thought youd have something fascinating to say. All I hear is a bunch of whining about something that you possibly can fix in the event you werent too busy searching for attention.
Normally I do not learn post on blogs, but I would like to say that this write-up very forced me to take a look at and do so! Your writing style has been amazed me. Thanks, quite nice post.
Very interesting information!Perfect just what I was looking for!
Whats up! I just want to give an enormous thumbs up for the nice info you could have here on this post. I will likely be coming back to your blog for extra soon.
I am glad for writing to make you know of the fabulous encounter my friend's princess developed studying your webblog. She mastered lots of details, most notably how it is like to have an ideal giving mindset to have many more smoothly fully grasp chosen complicated things. You really did more than our desires. Thank you for showing such useful, trustworthy, informative and even cool tips on that topic to Jane.
Thanks for another informative site. Where else could I get that kind of information written in such a perfect way? I've a project that I am just now working on, and I have been on the look out for such info.
Very interesting topic, appreciate it for posting.
An fascinating dialogue is price comment. I think that it is best to write more on this topic, it won't be a taboo subject but usually individuals are not enough to speak on such topics. To the next. Cheers
you have a great blog here! would you like to make some invite posts on my blog?
A powerful share, I just given this onto a colleague who was doing a little analysis on this. And he in truth bought me breakfast as a result of I found it for him.. smile. So let me reword that: Thnx for the treat! But yeah Thnkx for spending the time to discuss this, I really feel strongly about it and love studying extra on this topic. If doable, as you change into expertise, would you thoughts updating your blog with more details? It's highly useful for me. Huge thumb up for this blog publish!
Thank you for another magnificent post. Where else could anyone get that type of information in such an ideal way of writing? I have a presentation next week, and I am on the look for such information.
Hey! Do you know if they make any plugins to safeguard against hackers? I'm kinda paranoid about losing everything I've worked hard on. Any suggestions?
I like the efforts you have put in this, thanks for all the great blog posts.
You have brought up a very superb points, regards for the post.
Great ?V I should definitely pronounce, impressed with your site. I had no trouble navigating through all tabs and related info ended up being truly simple to do to access. I recently found what I hoped for before you know it at all. Reasonably unusual. Is likely to appreciate it for those who add forums or something, web site theme . a tones way for your client to communicate. Excellent task..
Do you have a spam issue on this site; I also am a blogger, and I was wanting to know your situation; many of us have developed some nice practices and we are looking to exchange strategies with other folks, why not shoot me an e-mail if interested.
What i do not understood is actually how you're not actually much more well-liked than you may be now. You're very intelligent. You realize thus significantly relating to this subject, produced me personally consider it from numerous varied angles. Its like men and women aren't fascinated unless it’s one thing to do with Lady gaga! Your own stuffs nice. Always maintain it up!
What i do not realize is in reality how you are no longer really a lot more neatly-liked than you may be now. You're very intelligent. You already know thus considerably with regards to this subject, made me individually consider it from numerous varied angles. Its like men and women aren't involved until it?¦s something to do with Girl gaga! Your own stuffs nice. At all times care for it up!
There are some fascinating points in time on this article but I don’t know if I see all of them heart to heart. There is some validity but I will take hold opinion till I look into it further. Good article , thanks and we wish extra! Added to FeedBurner as properly
Normally I do not read post on blogs, however I wish to say that this write-up very compelled me to check out and do it! Your writing taste has been amazed me. Thanks, quite great post.
I like this post, enjoyed this one regards for putting up. "We seldom attribute common sense except to those who agree with us." by La Rochefoucauld.
Very interesting information!Perfect just what I was looking for! "The medium is the message." by Marshall McLuhan.
You made some good points there. I looked on the internet for the topic and found most people will go along with with your site.
certainly like your website but you need to check the spelling on quite a few of your posts. Several of them are rife with spelling issues and I find it very troublesome to tell the truth nevertheless I will definitely come back again.
Hi, i read your blog occasionally and i own a similar one and i was just curious if you get a lot of spam remarks? If so how do you prevent it, any plugin or anything you can advise? I get so much lately it's driving me mad so any help is very much appreciated.