简单直观地理解神经网络

0 前言

本文为初步学习神经网络同学而准备，旨在通过最简单直观的方式建立初学者对于神经网络的印象。所以本文的结论和观点主要追求简单直观，而不是严谨。

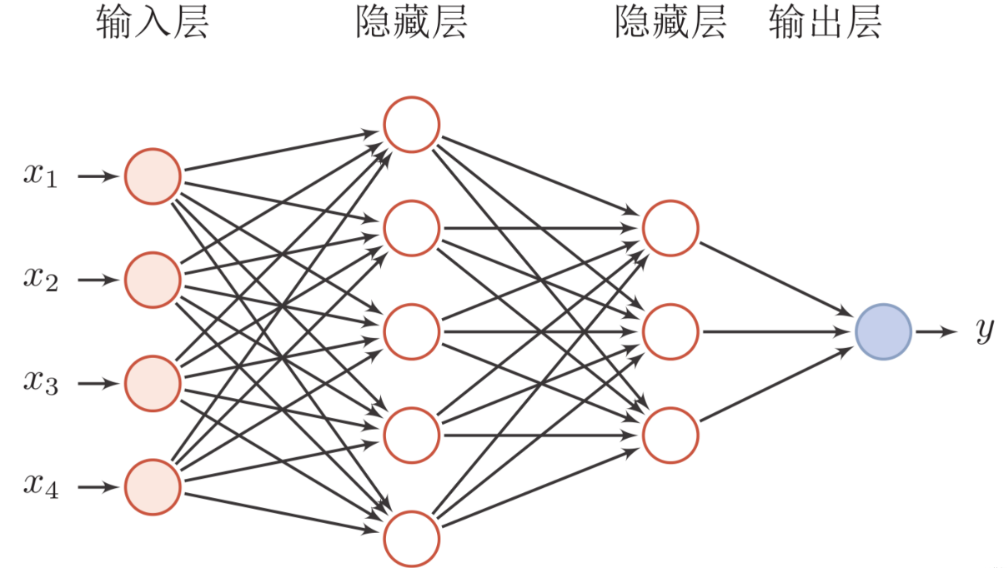
先举个简单的例子：

假设现在我们有输入 X 与对应输出 Y 的数据一堆 (X, Y) 对如下：

{ (1, 3), (2, 5), (3, 7), (4, 9), (5, 11), (6, 13), (7, 15), (8, 17), (9, 19), (10, 21) }

现在我们使用架构 f(x) = wx + b

如果我们把 f(x) 当做一个神经网络。那么，神经网络算法的目的，就是找到最优的参数 w 和 b，使得它们针对数据的误差损失最小。

可以发现，如果我们令 w = 2，b = 1，就能完美地拟合数据，误差损失最小。那么这个 w = 2，b = 1 就是我们想要找到的最优参数。

1 神经网络 = f(X)

神经网络本质上是一种数学模型，它通过一系列复杂的非线性变换（由不同的层和激活函数组成）来映射输入（X）到输出（Y）。

这里的 f 表示的就是这个从输入空间到输出空间的映射函数。神经网络通过学习调整其内部权重和偏置参数，以找到一个合适的函数f来逼近理想中的目标函数，从而对给定的输入 X 进行有效的预测或分类。

2 神经网络模型 = 模型架构 + 模型参数

神经网络模型是由“模型架构”和“模型参数”两个核心部分组成的。

• 模型架构：是神经网络的结构设计，包括但不限于网络的层数、每层的神经元数量、使用什么样的激活函数、网络的连接方式（例如全连接、卷积、循环等）等。模型架构决定了信息在神经网络中流动和变换的方式，以及网络能够学习到的特征的复杂度和类型。
• 模型参数：是神经网络学习过程中的可调节变量，主要包括权重（weights）和偏置（biases）。权重决定了每个神经元对前一层输出的重视程度，而偏置则是加在神经元上的一个常数项，用于调整激活函数的阈值。在训练过程中，通过优化算法（如梯度下降）调整这些参数，使得神经网络能够更好地拟合训练数据，从而在未知数据上表现得更好。

更通俗的，

• 模型架构一般指的是不同类型的神经网络，比如适用于图像的卷积神经网络，适用于文本的循环神经网络。不过我们一般口头上讲的什么什么模型，可能更偏向于指的是模型的架构。
• 模型参数指的是我们模型里一堆待定的数值。我们常常说的训练模型，这里的训练，到底是在做什么呢？事实上，训练本质想要做的就是一件事情，更新参数。我们不断更新参数，使得不同的输入有各自期望的输出。

3 训练 = 前向传播 + 反向传播 + 参数更新

• 前向传播：在这个阶段，输入数据从输入层经过隐藏层，一路向前直到输出层，每一层的神经元都会根据当前的权重和偏置进行计算，产生该层的输出，作为下一层的输入。这一过程最终产生一个预测输出，与实际标签进行比较以评估误差。
• 反向传播：计算预测输出与真实标签之间的误差，并从输出层开始，逆向地计算每一层的误差梯度。这个过程利用链式法则，逐层计算并累积权重和偏置的梯度，以便了解如何调整这些参数来减小损失函数的值。
• 参数更新：基于反向传播得到的梯度信息，使用优化算法（如梯度下降、随机梯度下降、Adam等）来调整网络中的权重和偏置，目标是逐步减小预测误差，使模型更好地拟合训练数据。

4 训练的目的 = 更新参数

我们一直在说的训练模型中的训练，本质就是想要更新参数。通过不断更新参数来最小化预测输出与实际标签之间的差距（即损失函数的值），从而提升模型在训练数据集上的表现，并期望泛化到未见数据时也能有良好的性能。

5 前向传播 = 计算和转换特征

前向传播过程中，输入数据经过神经网络每一层的计算，包括线性变换（权重和偏置的应用）和非线性变换（通过激活函数），从而逐渐从原始特征转换为更加抽象和高级的特征表示。

6 反向传播 = 计算误差梯度

反向传播的核心任务是计算误差梯度，即损失函数相对于模型参数的导数。这一步骤对于后续的参数更新至关重要，因为它指明了参数应该如何调整以减小网络的预测误差。

7 更新参数的核心思想

如何更新参数呢，由于我们希望不同的输入有各自期望的输出，所以，一种常见的方式是，给每一个输入都确定它希望的输出，这个我们期望的输出，我们称之为标签。标签就像一个向导，指导参数往使得模型效果更好的方向走，我们希望模型的输出不断地贴近输入对应的标签。

总结：神经网络就像一个函数 Z = f(X)。通常来讲（有监督），搭建神经网络模型解决问题，就是准备输入 X 和标签 Y，确定模型架构，通过训练不断更新模型参数，从而使得我们的模型的输出不断地贴近输入对应的标签（Z = Y）。