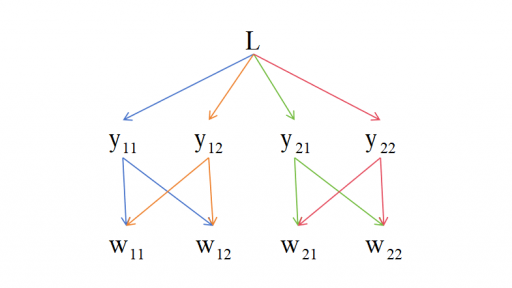
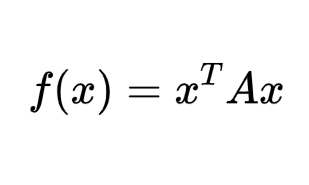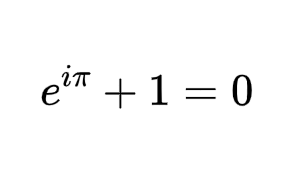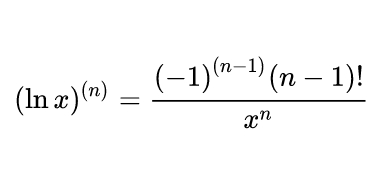0 前言 在初次接触神经网络的时候，不知道有没有人像我一样，对梯度计算的过程很模糊。可能大体上知道是使用链式法则来做，但是平常接触的都是一元复合函数的求导，像神经网络中这种对参数矩阵求导的具体细节完全不了解。 这篇文章从多元复合函数求导（矩阵求导的重要基础）入手，通过简单的例子进行切入，展示矩阵求导的完整细节。希望这篇文章对想要了解神经网络梯度计算细节的人有所帮助。 1 多元复合函数求导 首先我们先来介绍多元复合函数求导，这是矩阵求导的重要基础。 1.1 问题切入 问：考虑三个函数：， 以及 ，假设偏导都存在，我们…

0 前言 线性代数中涉及到的一个非常重要的内容是二次型，而二次型中涉及到的一个非常重要的内容是二次型化标准型。也许很多人对二次型化标准型非常熟悉，但是如果问到二次型化标准型有什么用，可能挺多人会愣一愣。这篇文章给大家带来的就是二次型的一个应用——最值求解。 1 二次型化标准型 下面先简单回顾下二次型、标准型、二次型化标准型 1.1 二次型 二次型是指含有 n 个变量 的二次齐次多项式，即在一个多项式中，未知数的个数为任意多个，但每一项的次数都为 2。它可以表示为如下形式： 或者更一般地表示为矩阵形式： 其中， 是变…

0 引言 在数学的浩瀚星空中，有一颗璀璨的星辰，以其无与伦比的简洁与深邃，被誉为“上帝最喜爱的公式”。本文将带你踏上一场探索之旅，揭开这一数学奇迹的神秘面纱。 1 五大常数 在数学中有这样五个常数： 0: 一切的起点与归宿，数学的虚空与全有。 1: 统一与存在的象征，数学运算的基石。 π: 圆周率，自然界无处不在的比例，连接直线与曲线的桥梁。 e: 自然对数的底，增长与变化的自然法则。 i: 虚数单位，超越实数范畴，开启复数世界的钥匙。 2 欧拉恒等式 而有这样一个公式，将数学中几个这几个看似不相关的常数——自然对…

0. 基础 n 阶四公式形式 二阶以及二阶以上的导数，统称高阶导数 高阶导数四大解法： 变形成 n 阶四公式形式 莱布尼茨公式（常需利用 n 阶四公式） 泰勒公式化得多项式 观察规律法 首先，要想解高阶导数又快又准，n 阶四公式绝对是基础中的基础，所以，请务必记住 n 阶四公式： （由 ，有 ） （ ） 所谓 n 阶四公式，即幂函数、指数函数、对数函数、三角函数最简单形式的 n 阶导数的值。 但是通常，题目不会直接让我们求这四个函数，一般我们要求的，都是 n 阶四公式形式的函数，比如说，求的是 ，，。 我们只要记住…