0 前言
在初次接触神经网络的时候,不知道有没有人像我一样,对梯度计算的过程很模糊。可能大体上知道是使用链式法则来做,但是平常接触的都是一元复合函数的求导,像神经网络中这种对参数矩阵求导的具体细节完全不了解。
这篇文章从多元复合函数求导(矩阵求导的重要基础)入手,通过简单的例子进行切入,展示矩阵求导的完整细节。希望这篇文章对想要了解神经网络梯度计算细节的人有所帮助。
1 多元复合函数求导
首先我们先来介绍多元复合函数求导,这是矩阵求导的重要基础。
1.1 问题切入
问:考虑三个函数:\(z = f(u, v)\),\(u = g(x, y)\) 以及 \(v = h(x, y)\),假设偏导都存在,我们的目标是求出 \(z\) 关于 \(x\) 的偏导 \(\frac{\partial z}{\partial x}\) 和 \(z\) 关于 \(y\) 的偏导 \(\frac{\partial z}{\partial y}\)。
解:我们可以先画出变量之间关系的依赖图如下:
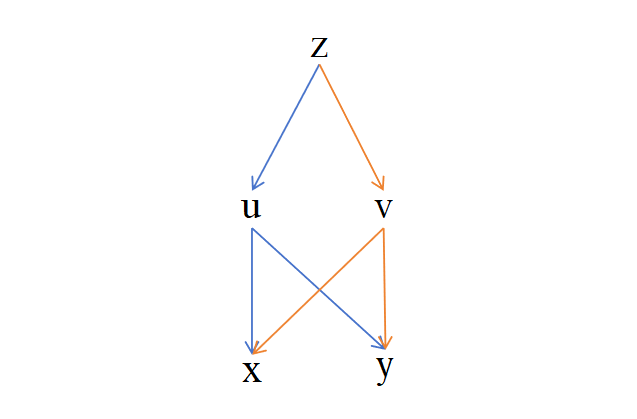
上述的依赖图对于我们理清楚变量之间关系,进而理清楚链式求导中的细节非常有帮助。根据上面的依赖图和链式求导法则,有
\(\frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x}\\\) \(\frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y}\)1.2 例子
我们举个更具体的例子:
问:假设有 \(z = u^2 + v^2\),其中 \(u = x + y\),\(v = x - y\),求 \(z\) 对 \(x\) 的偏导 \(\frac{\partial z}{\partial x}\) 和 \(z\) 对 \(y\) 的偏导 \(\frac{\partial z}{\partial y}\)。
解:z 对 u 和 v 的偏导分别为:
\(\frac{\partial z}{\partial u} = 2u\\\) \(\frac{\partial z}{\partial v} = 2v\)\(u\) 对 \(x\) 和 \(y\) 的偏导分别为:
\(\frac{\partial u}{\partial x} = 1\\\) \(\frac{\partial u}{\partial y} = 1\)\(v\) 对 \(x\) 和 \(y\) 的偏导分别为:
\(\frac{\partial v}{\partial x} = 1\\\) \(\frac{\partial v}{\partial y} = -1\)则有:
\(\frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} = 2u + 2v\\\) \(\frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y} = 2u - 2v\)2 梯度计算
2.1 问题
在神经网络算法中,都会涉及到求参数的梯度问题,也即求损失函数 L 对 参数矩阵 W 梯度问题。我们来看这类求参数梯度问题的一个例子:
问:考虑 \(L = (y_{11} - a_{11})^2 + (y_{12} - a_{12})^2 + (y_{21} - a_{21})^2 + (y_{22} - a_{22})^2\)
其中,
\(\begin{bmatrix}
y_{11} & y_{12} \\
y_{12} & y_{22}
\end{bmatrix}
=
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22}
\end{bmatrix}
\begin{bmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22}
\end{bmatrix}
(Y= WX)\)
求 \(L\) 对 \(W\) 的梯度 \(\frac{\partial L}{\partial W}\)。
2.2 问题转化
上面的问题本质其实还是多元复合函数求导问题,是我们最开始提到的例子的一个简单的扩展。我们调整一下问题的呈现方式,问题就变成了:
考虑 \(L = (y_{11} - a_{11})^2 + (y_{12} - a_{12})^2 + (y_{21} - a_{21})^2 + (y_{22} - a_{22})^2\)
其中,
\(y_{11} = w_{11}x_{11} + w_{12}x_{21}\\\) \(y_{12} = w_{11}x_{12} + w_{12}x_{22}\\\) \(y_{21} = w_{21}x_{11} + w_{22}x_{21}\\\) \(y_{12} = w_{11}x_{12} + w_{12}x_{22}\)求解:
\(\begin{bmatrix}\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}}
\end{bmatrix}\)
2.3 问题解决
前面提到了依赖图对于我们理清楚变量之间的依赖关系非常有帮助,上述函数中 \(L\)、\(y_{ij}\)、\(w_{ij}\) 有如下依赖关系:
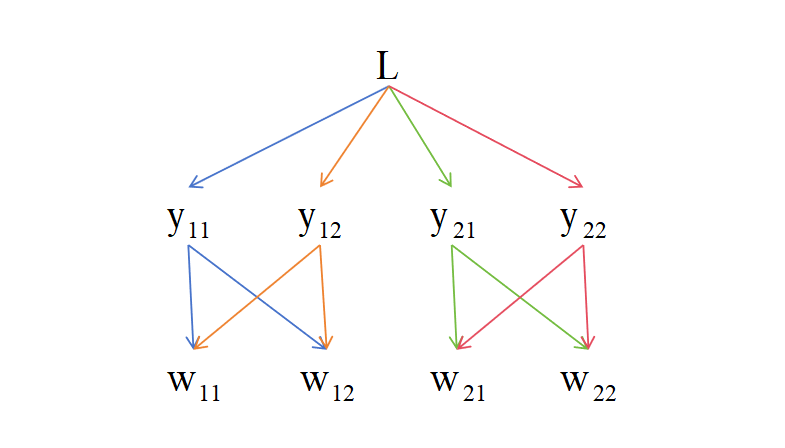
由上述依赖关系,有
\(\frac{\partial L}{\partial w_{11}} = \frac{\partial L}{\partial y_{11}} \frac{\partial y_{11}}{\partial w_{11}} + \frac{\partial L}{\partial y_{12}} \frac{\partial y_{12}}{\partial w_{11}}\\\) \(\frac{\partial L}{\partial w_{12}} = \frac{\partial L}{\partial y_{11}} \frac{\partial y_{11}}{\partial w_{12}} + \frac{\partial L}{\partial y_{12}} \frac{\partial y_{12}}{\partial w_{12}}\) \(\frac{\partial L}{\partial w_{21}} = \frac{\partial L}{\partial y_{21}} \frac{\partial y_{21}}{\partial w_{21}} + \frac{\partial L}{\partial y_{22}} \frac{\partial y_{22}}{\partial w_{21}}\\\) \(\frac{\partial L}{\partial w_{21}} = \frac{\partial L}{\partial y_{21}} \frac{\partial y_{21}}{\partial w_{22}} + \frac{\partial L}{\partial y_{22}} \frac{\partial y_{22}}{\partial w_{22}}\)\(L\) 对 \(y_{11}\)、 \(y_{12}\)、 \(y_{21}\)、 \(y_{22}\) 的偏导分别为
\(\frac{\partial L}{\partial y_{11}} = 2(y_{11}-a_{11})\\\) \(\frac{\partial L}{\partial y_{12}} = 2(y_{12}-a_{12})\\\) \(\frac{\partial L}{\partial y_{21}} = 2(y_{21}-a_{21})\\\) \(\frac{\partial L}{\partial y_{22}} = 2(y_{22}-a_{22})\)\(y_{11}\) 对 \(w_{11}\) 和 \(w_{12}\) 的偏导分别为
\(\frac{\partial y_{11}}{\partial w_{11}} = x_{11}\\\) \(\frac{\partial y_{11}}{\partial w_{12}} = x_{21}\)\(y_{12}\) 对 \(w_{11}\) 和 \(w_{12}\) 的偏导分别为
\(\frac{\partial y_{12}}{\partial w_{11}} = x_{12}\\\) \(\frac{\partial y_{12}}{\partial w_{12}} = x_{22}\)\(y_{21}\) 对 \(w_{21}\) 和 \(w_{22}\) 的偏导分别为
\(\frac{\partial y_{21}}{\partial w_{21}} = x_{11}\\\) \(\frac{\partial y_{21}}{\partial w_{22}} = x_{21}\)\(y_{22}\) 对 \(w_{21}\) 和 \(w_{22}\) 的偏导分别为
\(\frac{\partial y_{22}}{\partial w_{21}} = x_{12}\\\) \(\frac{\partial y_{22}}{\partial w_{22}} = x_{22}\)因此
\(\frac{\partial L}{\partial w_{11}} = \frac{\partial L}{\partial y_{11}} \frac{\partial y_{11}}{\partial w_{11}} + \frac{\partial L}{\partial y_{12}} \frac{\partial y_{12}}{\partial w_{11}} = 2(y_{11}-a_{11})x_{11} + 2(y_{12}-a_{12})x_{12}\) \(\frac{\partial L}{\partial w_{12}} = \frac{\partial L}{\partial y_{11}} \frac{\partial y_{11}}{\partial w_{12}} + \frac{\partial L}{\partial y_{12}} \frac{\partial y_{12}}{\partial w_{12}} = 2(y_{11}-a_{11})x_{21} + 2(y_{12}-a_{12})x_{22}\) \(\frac{\partial L}{\partial w_{21}} = \frac{\partial L}{\partial y_{21}} \frac{\partial y_{21}}{\partial w_{21}} + \frac{\partial L}{\partial y_{22}} \frac{\partial y_{22}}{\partial w_{21}} = 2(y_{21}-a_{21})x_{11} + 2(y_{22}-a_{22})x_{12}\) \(\frac{\partial L}{\partial w_{21}} = \frac{\partial L}{\partial y_{21}} \frac{\partial y_{21}}{\partial w_{22}} + \frac{\partial L}{\partial y_{22}} \frac{\partial y_{22}}{\partial w_{22}} = 2(y_{21}-a_{21})x_{21} + 2(y_{22}-a_{22})x_{22}\)整理得
\(\begin{bmatrix}\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}}
\end{bmatrix}
\\=
\begin{bmatrix}
2(y_{11}-a_{11})x_{11} + 2(y_{12}-a_{12})x_{12} & 2(y_{11}-a_{11})x_{21} + 2(y_{12}-a_{12})x_{22} \\
2(y_{21}-a_{21})x_{11} + 2(y_{22}-a_{22})x_{12} & 2(y_{21}-a_{21})x_{21} + 2(y_{22}-a_{22})x_{22}
\end{bmatrix}
\\=
\begin{bmatrix}
2(y_{11}-a_{11}) & 2(y_{12}-a_{12}) \\
2(y_{21}-a_{21}) & 2(y_{22}-a_{22})
\end{bmatrix}
\begin{bmatrix}
x_{11} & x_{21} \\
x_{12} & x_{22}
\end{bmatrix}\)
至此,我们已经成功求解了 \(L\) 对 \(W\) 的梯度,如果是在神经网络中就可以根据这个梯度更新参数值了。
3 结束
事实上,在上面例子中,我们还能发现
\(\frac{\partial L}{\partial W} = \frac{\partial L}{\partial Y} \frac{\partial Y}{\partial W}\)并且,在 \(Y = W X\) 时, 有
\(\frac{\partial Y}{\partial W} =\begin{bmatrix}
x_{11} & x_{21} \\
x_{12} & x_{22}
\end{bmatrix}
= X^T\)
希望通过这篇文章,大家能明白矩阵求导的本质还是多元复合函数求导,以及如何通过画依赖图的方式,理清矩阵求导具体的链式细节。
感谢观看,希望对大家有启发和帮助。

文章评论
Heya i am for the first time here. I found this board and I find It truly useful & it helped me out much. I hope to give something back and help others like you helped me.
I really appreciate this post. I’ve been looking everywhere for this! Thank goodness I found it on Bing. You have made my day! Thank you again
Hello my friend! I wish to say that this post is amazing, nice written and include approximately all important infos. I’d like to see more posts like this.
Whoa! This blog looks exactly like my old one! It's on a totally different subject but it has pretty much the same layout and design. Superb choice of colors!
Good blog! I really love how it is easy on my eyes and the data are well written. I'm wondering how I might be notified whenever a new post has been made. I've subscribed to your RSS feed which must do the trick! Have a nice day!
Great write-up, I'm regular visitor of one's website, maintain up the nice operate, and It is going to be a regular visitor for a lengthy time.
You actually make it seem really easy with your presentation however I in finding this topic to be actually one thing that I feel I'd by no means understand. It seems too complex and very extensive for me. I'm looking forward in your next submit, I¦ll attempt to get the grasp of it!
I really like your writing style, fantastic information, appreciate it for putting up :D. "Inquiry is fatal to certainty." by Will Durant.
Utterly written content material, thanks for information .
I used to be very happy to search out this internet-site.I needed to thanks on your time for this wonderful learn!! I undoubtedly enjoying each little bit of it and I have you bookmarked to check out new stuff you blog post.
I haven¦t checked in here for a while because I thought it was getting boring, but the last several posts are great quality so I guess I¦ll add you back to my everyday bloglist. You deserve it my friend :)
There are some interesting cut-off dates in this article but I don’t know if I see all of them middle to heart. There's some validity however I'll take maintain opinion till I look into it further. Good article , thanks and we wish more! Added to FeedBurner as nicely
I simply couldn't leave your web site prior to suggesting that I extremely loved the usual info an individual provide for your visitors? Is gonna be back often to check up on new posts
Enjoyed looking at this, very good stuff, thankyou. "What the United States does best is to understand itself. What it does worst is understand others." by Carlos Fuentes.
whoah this blog is great i love reading your articles. Keep up the great work! You know, lots of people are hunting around for this information, you could help them greatly.
Woh I love your content, saved to bookmarks! .
I haven't checked in here for a while since I thought it was getting boring, but the last several posts are good quality so I guess I will add you back to my everyday bloglist. You deserve it my friend :)
I’m not sure where you are getting your information, however great topic. I needs to spend some time studying more or working out more. Thank you for wonderful info I used to be on the lookout for this information for my mission.
What i do not understood is in truth how you are now not actually much more neatly-preferred than you might be right now. You are so intelligent. You already know thus significantly when it comes to this matter, produced me individually consider it from numerous numerous angles. Its like men and women are not interested until it's something to accomplish with Girl gaga! Your own stuffs great. Always care for it up!
I'm really loving the theme/design of your weblog. Do you ever run into any browser compatibility issues? A couple of my blog readers have complained about my site not working correctly in Explorer but looks great in Chrome. Do you have any tips to help fix this problem?
My brother suggested I might like this website. He used to be entirely right. This post actually made my day. You cann't imagine simply how a lot time I had spent for this information! Thanks!
Keep working ,great job!
Thank you for another informative web site. Where else could I get that type of information written in such an ideal way? I've a project that I'm just now working on, and I've been on the look out for such info.
I really like reading and I conceive this website got some genuinely utilitarian stuff on it! .
I was looking at some of your posts on this internet site and I conceive this web site is real informative! Retain posting.
Rattling nice layout and good content, nothing at all else we want : D.
This website is really a stroll-by way of for all the info you needed about this and didn’t know who to ask. Glimpse right here, and you’ll definitely discover it.
I discovered your blog site on google and check just a few of your early posts. Proceed to keep up the excellent operate. I just further up your RSS feed to my MSN Information Reader. Seeking ahead to reading more from you later on!…
Hello my family member! I want to say that this post is amazing, great written and come with approximately all important infos. I would like to look more posts like this .