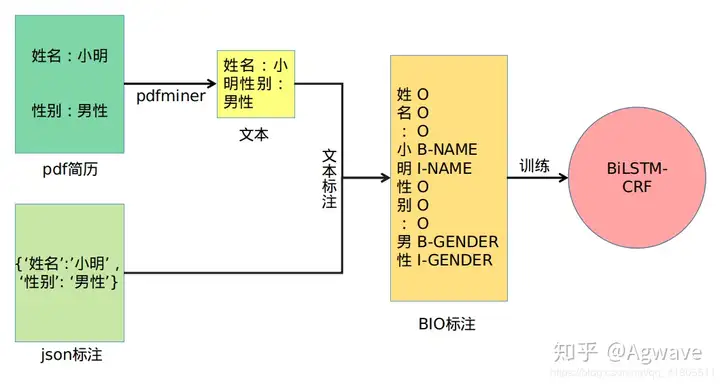
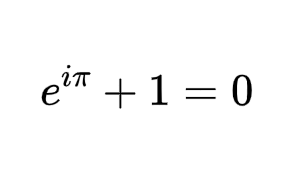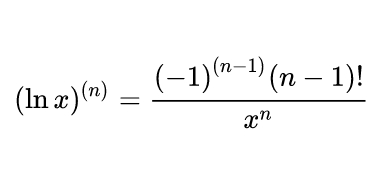0. 摘要 参加了天池的一个pdf简历信息提取的比赛，这里进行回顾、整理和分享 赛题要求从pdf简历中提取出信息，比如说名字，籍贯等。这里搭建了一个BiLSTM-CRF模型，能够从PDF简历中提取出所需的信息。 模型的线上得分是0.727，排名 21/1200+ 1. 赛题相关 模型目标：pdf简历 --> 类别信息 2. 思路 使用python库pdfminer，将pdf简历中的文本提取出来。利用json标注文件，对提取出来的文本进行匹配和BIO标注，每一个字对应一个标注。最后，将标注后的文本送到BiLSM…

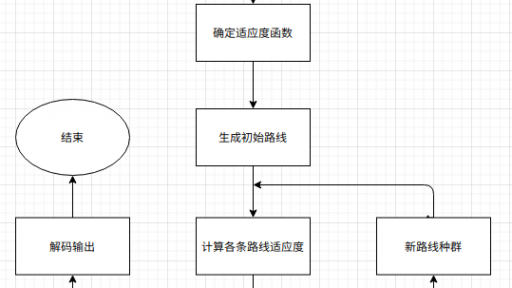
1 问题描述 旅行商问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。 本文章中，城市数据为 127 个城市的 x 和 y 坐标。数据地址见文末。 2 流程图 3 实现细节解释 3.1 路线个体的表示 采用整数编码的方式，将 n 个城市依次编码为 0 到 n-1。对于所给数据而言，将127个城市依次编码为0至126。因此，一条路线可以由一个127维的向量进行表示。 由于路线需要频繁更改，但不会增加或减少城市，这里采用 numpy 作为存储结构。 在实际编码中，为了提高运行效率…

0 引言 在数学的浩瀚星空中，有一颗璀璨的星辰，以其无与伦比的简洁与深邃，被誉为“上帝最喜爱的公式”。本文将带你踏上一场探索之旅，揭开这一数学奇迹的神秘面纱。 1 五大常数 在数学中有这样五个常数： 0: 一切的起点与归宿，数学的虚空与全有。 1: 统一与存在的象征，数学运算的基石。 π: 圆周率，自然界无处不在的比例，连接直线与曲线的桥梁。 e: 自然对数的底，增长与变化的自然法则。 i: 虚数单位，超越实数范畴，开启复数世界的钥匙。 2 欧拉恒等式 而有这样一个公式，将数学中几个这几个看似不相关的常数——自然对…

0. 基础 n 阶四公式形式 二阶以及二阶以上的导数，统称高阶导数 高阶导数四大解法： 变形成 n 阶四公式形式 莱布尼茨公式（常需利用 n 阶四公式） 泰勒公式化得多项式 观察规律法 首先，要想解高阶导数又快又准，n 阶四公式绝对是基础中的基础，所以，请务必记住 n 阶四公式： （由 ，有 ） （ ） 所谓 n 阶四公式，即幂函数、指数函数、对数函数、三角函数最简单形式的 n 阶导数的值。 但是通常，题目不会直接让我们求这四个函数，一般我们要求的，都是 n 阶四公式形式的函数，比如说，求的是 ，，。 我们只要记住…