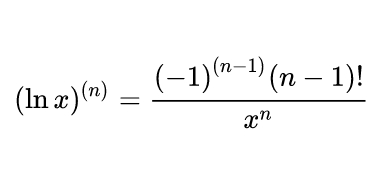0. 基础 n 阶四公式形式 二阶以及二阶以上的导数,统称高阶导数 高阶导数四大解法: 变形成 n 阶四公式形式 莱布尼茨公式(常需利用 n 阶四公式) 泰勒公式化得多项式 观察规律法 首先,要想解高阶导数又快又准,n 阶四公式绝对是基础中的基础,所以,请务必记住 n 阶四公式: (由 ,有 ) ( ) 所谓 n 阶四公式,即幂函数、指数函数、对数函数、三角函数最简单形式的 n 阶导数的值。 但是通常,题目不会直接让我们求这四个函数,一般我们要求的,都是 n 阶四公式形式的函数,比如说,求的是 ,,。 我们只要记住…
陈银波
邮箱:agwave@foxmail.com
知乎:https://www.zhihu.com/people/agwave
github:https://github.com/agwave
leetcode:https://leetcode.cn/u/agwave
最近评论
bggbet 发布于 19 小时前(01月08日)
远程桌面 发布于 2 天前(01月07日)
爱思助手下载 发布于 2 天前(01月07日)
victor96 casino login 发布于 3 天前(01月06日)
https://dondeesta.biz/ 发布于 4 天前(01月05日)
搜索