图注意力网络（GAT）：一个例子解释从输入到输出维度变化的完整过程

7 7 月, 2024 2760点热度 5人点赞 2条评论

0 前言

我不知道大家有没有和我一样的感受，很多论文里面的神经网络架构往往是通过一系列数学公式来表达，这本身没有问题，但对于初步想要完整了解整个网络架构的人来说，往往就要花比较多的时间去理解公式。

而当我在了解一个神经网络架构的时候，只有完全清楚输入到输出的完整过程，特别是张量维度变化的完整过程，才算认为自己确实了解了这个网络架构。所以我学习的时候往往希望有人能给我个例子，完整展示输入到输出的情况，让我能够更快地去理解论文的架构。我感觉可能也有人和我有同样的需求，所以这篇文章应运而生。这篇文章通过一个的例子，完整地展示 GAT 架构是如何将输入逐步转换为输出的。

如果大家觉得这种通过例子学习方式对自己帮助，请点赞或者评论让我知道，我会继续更新这种类型的文章。

1 公式

1.1 GAT 公式

GAT 更新当前节点特征的公式如下：

\(\overrightarrow{h_{i}'} = \sigma \left( \frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_i} \alpha^{k}_{ij} W^k \overrightarrow{h_j} \right)\)

这个公式描述了图注意力网络中一个节点的特征向量更新过程。看着好像很复杂，其实还好，我们来逐项解释下：

\(\overrightarrow{h_{i}'}\)：这表示经过 GAT 层变换后，节点 \(i\) 的新特征向量，记维度为 \(F'\)，该维度大小与 \(W^k\) 相关。这里的箭头表示它是一个向量。
\(\sigma\)：这是一个激活函数，用于添加非线性特性到模型中。常用的激活函数有 ReLU、tanh 等。它作用于括号内的求和结果上。
\(\frac{1}{K}\)：这是一个缩放因子，用于在有多个注意力头的情况下平均它们的输出。\(K\) 代表注意力头的数量，这样可以捕捉不同类型的注意力关系。
\(\sum_{k=1}^{K}\)：这个求和符号表示对于每一个注意力头 \(k\)，都会执行内部的计算并最后将结果相加。这样做允许模型学习多种类型的节点间关系。
\(\sum_{j \in \mathcal{N}_i}\)：这个求和符号表示对节点 \(i\) 的所有邻居节点 \(j\) 进行遍历和累加操作，其中 \(\mathcal{N}_i\) 表示节点 \(i\) 的一阶邻域，即与节点 \(i\) 直接相连的所有节点集合。
\(\alpha^{k}_{ij}\)：这是注意力系数，表示在第 \(k\) 个注意力头下，节点 \(i\) 对邻居节点 \(j\) 的关注程度。它是通过一个注意力机制学习得到的，能够动态地调整邻居节点对中心节点的影响权重。高的 \(\alpha^{k}_{ij}\) 值意味着节点 \(j\) 对节点 \(i\) 的影响大。
\(W^k\)：这是一个权重矩阵，对应于第 \(k\) 个注意力头的可学习参数。记维度为 \(F' \times F \)，它会被应用于邻居节点 \(j\) 的特征向量 \(\overrightarrow{h_j}\)，以变换其特征空间，使得模型能够学习更复杂的节点间交互模式。
\(\overrightarrow{h_j}\)：这是邻居节点 \(j\) 的原始特征向量，在被注意力机制加权之前。记维度为 \(F\)。

其中，\(\alpha^{k}_{ij}\) 是通过注意力公式计算得来。下面我们来介绍注意力公式。

1.2 注意力公式

\(\alpha^k_{ij} = \frac{exp \left( {LeakyReLU \left( \overrightarrow{\text{a}^k}^T \left[ W^k \overrightarrow{h_i} || W^k \overrightarrow{h_j} \right] \right )} \right )}{\sum_{l \in \mathcal{N}_i} exp \left ({LeakyReLU \left( \overrightarrow{\text{a}^k}^T \left[ W^k \overrightarrow{h_i} || W^k \overrightarrow{h_l} \right] \right )} \right )}\)

这个公式定义了图注意力网络（GAT）中计算两个节点之间注意力权重的方法。下面是各个部分的详细解释：

\(\alpha^k_{ij}\)：表示在第 \(k\) 个注意力头下，节点 \(i\) 对邻居节点 \(j\) 的注意力权重。
\(\overrightarrow{\text{a}^k}\)：是第 \(k\) 个注意力头特有的可学习权重向量，用于计算该头的注意力分数。如果更新后的特征向量维度记为 \(F'\)，则其维度为 \(2F'\)
\(W^k\)：是与第 \(k\) 个注意力头相关的权重矩阵，用于将节点特征从原始特征空间映射到该头特有的特征空间。记维度为 \(F' \times F \)。此处的 \(W^k\) 与上个公式（GAT 公式）的 \(W^k\) 是同一个。
\(W^k \overrightarrow{h_i} || W^k \overrightarrow{h_j}\)：表示将节点 \(i\) 和节点 \(j\) 的特征通过第 \(k\) 个注意力头的权重矩阵变换后拼接在一起，作为注意力机制的输入。
exp 与 LeakyReLU：分子中的 exp 和 LeakyReLU 组合使用，计算了节点 \(i\) 到节点 \(j\) 在第 \(k\) 个注意力头下的未归一化注意力分数。
\(\sum_{l \in \mathcal{N}_i}\)：分母中的求和是对节点 \(i\) 的所有邻居节点 \(l\) 执行相同操作后结果的总和，用来进行 softmax 归一化，确保所有邻居节点关于头 \(k\) 的注意力权重之和为1。

2 例子

假设现在有一份图数据如下

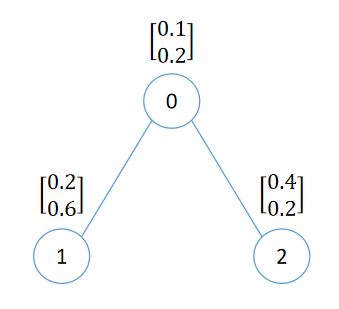
我们来看看对于这个图数据，如何计算和更新节点 0 的特征向量。在这个例子中，我们使用两个注意力头，即 \(K=2\)），并且我们假设线性变换后的特征向量维度 \(F' = 3\)。

2.1 注意力公式例子

我们先来看注意力公式如何用来计算权重。

其中，特征向量

\(h_0 = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix}\\\) \(h_1 = \begin{bmatrix} 0.2 \\ 0.6 \end{bmatrix}\\\) \(h_2 = \begin{bmatrix} 0.4 \\ 0.2 \end{bmatrix}\)

\(W^k\) 是可学习的权重矩阵，由原始特征向量维度知 \(F = 2\)，线性变换后的特征向量维度 \(F' = 3\)，则 \(W^k\) 的维度为 \(F' \times F\)。我们可以进行如下初始化：

\(W^1 = \begin{bmatrix} 0.4 & 0.4 \\ 0.4 & 0.4 \\ 0.4 & 0.4 \end{bmatrix}\\\) \(W^2 = \begin{bmatrix} 0.2 & 0.2 \\ 0.2 & 0.2 \\ 0.2 & 0.2 \end{bmatrix}\\\)

\(\overrightarrow{\text{a}^k}\) 是可学习的权重向量，由线性变换后的的特征向量维度为 \(F' = 3\)，则该向量的维度为 \(2F' = 6\)。我们可以进行如下初始化：

\(\overrightarrow{\text{a}^1} = \begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}\\\) \(\overrightarrow{\text{a}^2} = \begin{bmatrix} 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \end{bmatrix}\\\)

则当 \(k = 1\) 时有

\(W^1 \overrightarrow{h_0} = \begin{bmatrix} 0.4 & 0.4 \\ 0.4 & 0.4 \\ 0.4 & 0.4 \end{bmatrix} \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \end{bmatrix}\\\) \(W^1 \overrightarrow{h_1} = \begin{bmatrix} 0.4 & 0.4 \\ 0.4 & 0.4 \\ 0.4 & 0.4 \end{bmatrix} \begin{bmatrix} 0.2 \\ 0.6 \end{bmatrix} = \begin{bmatrix} 0.32 \\ 0.32 \\ 0.32 \end{bmatrix}\\\) \(W^1 \overrightarrow{h_2} = \begin{bmatrix} 0.4 & 0.4 \\ 0.4 & 0.4 \\ 0.4 & 0.4 \end{bmatrix} \begin{bmatrix} 0.4 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 0.24 \\ 0.24 \\ 0.24 \end{bmatrix}\\\) \(\overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_1} \right] = {\begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}}^T \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \\ 0.32 \\ 0.32 \\ 0.32 \end{bmatrix} = 0.66\\\) \(\overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_2} \right] = {\begin{bmatrix} 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \\ 0.5 \end{bmatrix}}^T \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \\ 0.24 \\ 0.24 \\ 0.24 \end{bmatrix} = 0.54\\\)

进而

\(\alpha^1_{01} = \frac{exp \left( {LeakyReLU \left( \overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_1} \right] \right )} \right )}{\sum_{l \in \mathcal{N}_0} exp \left ({LeakyReLU \left( \overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_l} \right] \right )} \right )} = \frac{e^{0.66}}{e^{0.66}+e^{0.54}} \approx 0.53\) \(\alpha^1_{02} = \frac{exp \left( {LeakyReLU \left( \overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_2} \right] \right )} \right )}{\sum_{l \in \mathcal{N}_0} exp \left ({LeakyReLU \left( \overrightarrow{\text{a}^1}^T \left[ W^1 \overrightarrow{h_0} || W^1 \overrightarrow{h_l} \right] \right )} \right )} = \frac{e^{0.54}}{e^{0.66}+e^{0.54}} \approx 0.47\)

同理当 \(k = 2\) 时有

\(W^2 \overrightarrow{h_0} = \begin{bmatrix} 0.2 & 0.2 \\ 0.2 & 0.2 \\ 0.2 & 0.2 \end{bmatrix} \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 0.06 \\ 0.06 \\ 0.06 \end{bmatrix}\\\) \(W^2 \overrightarrow{h_1} = \begin{bmatrix} 0.2 & 0.2 \\ 0.2 & 0.2 \\ 0.2 & 0.2 \end{bmatrix} \begin{bmatrix} 0.2 \\ 0.6 \end{bmatrix} = \begin{bmatrix} 0.16 \\ 0.16 \\ 0.16 \end{bmatrix}\\\) \(W^2 \overrightarrow{h_2} = \begin{bmatrix} 0.2 & 0.2 \\ 0.2 & 0.2 \\ 0.2 & 0.2 \end{bmatrix} \begin{bmatrix} 0.4 \\ 0.2 \end{bmatrix} = \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \end{bmatrix}\\\) \(\overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_1} \right] = {\begin{bmatrix} 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \end{bmatrix}}^T \begin{bmatrix} 0.06 \\ 0.06 \\ 0.06 \\ 0.16 \\ 0.16 \\ 0.16 \end{bmatrix} = 0.396\\\) \(\overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_2} \right] = {\begin{bmatrix} 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \\ 0.6 \end{bmatrix}}^T \begin{bmatrix} 0.06 \\ 0.06 \\ 0.06 \\ 0.12 \\ 0.12 \\ 0.12 \end{bmatrix} = 0.324\\\)

进而

\(\alpha^2_{01} = \frac{exp \left( {LeakyReLU \left( \overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_1} \right] \right )} \right )}{\sum_{l \in \mathcal{N}_0} exp \left ({LeakyReLU \left( \overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_l} \right] \right )} \right )} = \frac{e^{0.396}}{e^{0.396}+e^{0.324}} \approx 0.52\\\) \(\alpha^2_{02} = \frac{exp \left( {LeakyReLU \left( \overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_2} \right] \right )} \right )}{\sum_{l \in \mathcal{N}_0} exp \left ({LeakyReLU \left( \overrightarrow{\text{a}^2}^T \left[ W^2 \overrightarrow{h_0} || W^2 \overrightarrow{h_l} \right] \right )} \right )} = \frac{e^{0.324}}{e^{0.396}+e^{0.324}} \approx 0.48\)

2.2 GAT 公式例子

GAT 公式为：

\(\overrightarrow{h_{i}'} = \sigma \left( \frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_i} \alpha^{k}_{ij} W^k \overrightarrow{h_j} \right)\)

则对于上面的例子(\(i = 0\), \(K = 2\))，有

\(\overrightarrow{h_{0}'} = \sigma \left( \frac{1}{2} \left( \left( \alpha^{1}_{01} W^1 \overrightarrow{h_1} + \alpha^{1}_{02} W^1 \overrightarrow{h_2}\right) + \left( \alpha^{2}_{01} W^2 \overrightarrow{h_1} + \alpha^{2}_{02} W^2 \overrightarrow{h_2} \right) \right) \right)\)

由前面的计算结果有

\(\alpha^{1}_{01} \approx 0.53\\\) \(W^1 \overrightarrow{h_1} = \begin{bmatrix} 0.32 \\ 0.32 \\ 0.32 \end{bmatrix}\\\) \(\alpha^{1}_{02} \approx 0.47\\\) \(W^1 \overrightarrow{h_2} = \begin{bmatrix} 0.24 \\ 0.24 \\ 0.24 \end{bmatrix}\\\) \(\alpha^{2}_{01} \approx 0.52\\\) \(W^2 \overrightarrow{h_1} = \begin{bmatrix} 0.16 \\ 0.16 \\ 0.16 \end{bmatrix}\\\) \(\alpha^{2}_{02} \approx 0.48\\\) \(W^2 \overrightarrow{h_2} = \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \end{bmatrix}\\\)

则

\(\overrightarrow{h_{0}'} = \sigma \left( \frac{1}{2} \left( \left( 0.53 * \begin{bmatrix} 0.32 \\ 0.32 \\ 0.32 \end{bmatrix} + 0.47 * \begin{bmatrix} 0.24 \\ 0.24 \\ 0.24 \end{bmatrix} \right) + \left( 0.52 * \begin{bmatrix} 0.16 \\ 0.16 \\ 0.16 \end{bmatrix} + 0.48 * \begin{bmatrix} 0.12 \\ 0.12 \\ 0.12 \end{bmatrix} \right) \right) \right) \\ = \begin{bmatrix} 0.2116 \\ 0.2116 \\ 0.2116 \end{bmatrix}\)

至此，我们对节点 0 的特征向量更新完毕，其他节点也进行类似更新。当所有节点的特征向量更新完成，GAT 层网络的前向传播也就完成了。这就是 GAT 层的完整细节。

希望我举的这个例子，能让你更简单深入地了解 GAT 网络的计算过程，尤其是维度变化的过程，也就不枉我“拼命地”计算了。

最后再留一个问题，如果我令注意力头数量为 3，更新后的特征向量长度为 4，那么计算过程有哪些变化呢？